§ 31. Замечания об анализе случайных процессов

 

В этом параграфе обсуждаются некоторые вопросы, относящиеся к технике спектрального анализа случайных процессов и к погрешностям, возникающим при анализе, т.е. при экспериментальном определении спектров. Для простоты будем иметь в виду только стационарные эргодические процессы.

Прежде всего заметим, что, как указывалось выше, в условиях эксперимента мы имеем дело обычно с одной из реализаций случайного процесса. Поэтому в основе действия анализаторов спектра случайных процессов лежит определение спектра, содержащее усреднение по времени, например

                                                              (31.1)

где

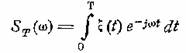
— текущий спектр реализации, а величина

выражает текущий спектр энергии, выделяемой процессом ξ(t) за время Т. Величина же

есть спектральная плотность средней за время Т мощности процесса ξ(t). Как |S_T(ω)|, так и G_T(ω) — случайные величины. Лишь в пределе G_T сходится к G, т.е.

                                                                        (31.2)

Совершенно ясно, что в условиях реального эксперимента мы располагаем только конечным временем T. Поэтому в результате однократного опыта мы получаем случайную величину G_T(ω), которая, вообще говоря, отличается от истинного значения G(ω). Если же опыт (одной и той же длительности Т) повторяется многократно, то получается множество значений G_T (ω) и в пределе мы могли бы найти истинный спектр, как

                                                                            (31.3)

Перейдем теперь к определению погрешности измерения, т.е. уклонения измеренного спектра от истинного его значения. Сначала определим энергию, выделяемую процессом ξ(t) за время Т. Эта энергия равна

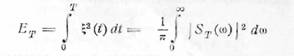
или

Очевидно, что и Е_т — случайная величина. Ее среднее значение есть

Средний квадрат уклонения Е_T от Е — это и есть средний квадрат ошибки измерения. Таким образом, средний квадрат ошибки выражается непосредственно дисперсией величины Е_T

                                   (31.4)

Мы имеем

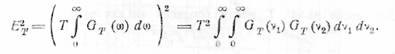
Для среднего значения этой величины Райс [29] выводит следующее выражение:

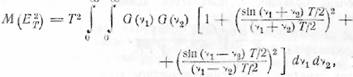                                 (31.5)

откуда

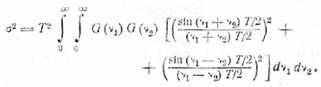                                       (31.6)

Удобнее нормировать ошибку, т.е. ввести среднеквадратичную относительную ошибку, определив ее как

ε = σ/E.

Теперь представим себе анализатор в виде идеального фильтра с коэффициентом передачи, равным единице в полосе частот от ω₁ до ω₂ и равным нулю вне этого интервала. Процесс анализа состоит в измерении энергии, выделяемой на выходе фильтра за время Т. Если анализатор имеет высокую разрешающую способность, то полоса

Ω = ω₁ ─ ω₂

узка, и мы можем считать, что в пределах этой полосы истинная спектральная плотность постоянна и равна g₀. В таком случае

а для среднего квадрата погрешности имеем

Для очень малых Т имеем (полагая sin x/x ≈ 1)

и

для очень больших Т получается асимптотическое выражение

Следует заметить, что асимптотическое выражение вида

имеет силу не только для идеального фильтра, который мы рассматриваем, но и для других типов фильтров; постоянная А зависит от свойства фильтра [21].

Для случая полосы, ширина которой мала по сравнению со средней частотой, т.е. при условии

подсчитаны 129] значения относительной погрешности как функции аргумента  (выкладки Раиса очень громоздки, и мы их не приводим); график этой зависимости представлен на рис. 55.

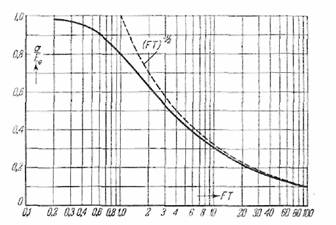
Рис. 55.

Как видим, ошибка убывает с возрастанием Т очень медленно. Ошибка тем больше, чем меньше F. Так, например, для того чтобы ошибка была меньше 10%, нужно взять FT = 100; при разрешающей способности 100 гц измерение должно продолжаться не менее одной секунды.

Заметим, что формула (31.6) выражает погрешность через истинный спектр G(ω), который неизвестен, так как он-то и должен быть определен в результате измерений. Возникающая здесь принципиальная трудность обойдена путем предположения, что спектральная плотность постоянна в узкой полосе Ω. Вычислить погрешность только на основании результатов измерения спектра нельзя принципиально. Для вычисления погрешности нужно знать нечто большее, а именно корреляцию спектра, который является моментом второго порядка; нужно, следовательно, измерять моменты четвертого порядка. Подробности можно найти в специальных работах по этому вопросу [20, 21].

Обратимся теперь к вопросам методики и техники спектрального анализа случайных процессов. Прежде всего отметим, что из основного определения спектра случайного процесса

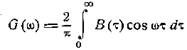
вытекает возможность косвенного измерения спектра, состоящая в том, что из опыта находится функция корреляции В(τ), а затем спектр получается путем преобразования Фурье (которое может выполняться либо путем численной обработки экспериментальных данных, либо при помощи того или иного прибора, выполняющего преобразование Фурье). При таком способе нахождения спектра в качестве основного измерительного прибора применяется не анализатор, а коррелометр. По вопросам измерения функций корреляции имеется обширная литература, обзор которой выходит за рамки нашей темы. Заметим лишь, что существует мнение [6], что определение спектра через функцию корреляции более экономно с точки зрения суммы требуемых измерительных и вычислительных операций, нежели прямое измерение спектра.

Что же касается методов непосредственного анализа, то простейший анализатор представляется в виде набора полосовых фильтров; в качестве выходных индикаторов должны применяться интегрирующие квадратичные приборы, измеряющие энергию. Это — наиболее чистый способ измерения, так как применение ваттметров сводится по существу к интегрированию с весом; весовая функция зависит от свойств как самого прибора, так и схемы его включения, что вносит элемент произвола в результат измерения. Точнее говоря, результат измерения представляет собой величину, определение которой вытекает из свойств измерительного устройства. Пример такого специализированного определения можно видеть в уже цитированной работе Фано [22].

Другой возможный способ анализа состоит в том, что измеряется энергия на выходе фильтра нижних частот с подвижной верхней границей, т.е. энергия в полосе от 0 до ω. Эта энергия равна

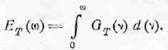
Если найденную функцию продифференцировать по частоте, то получим

Возможно применение приема, вообще очень употребительного в технике анализа, а именно периодическое повторение образца анализируемого процесса. Практически это осуществляется путем записи, например, на магнитной ленте, с последующим склеиванием достаточно длинного отрезка записи в кольцо. В месте склейки образуется, разумеется, разрыв если не самой функции, то ее производных. Это обстоятельство оказывает на результат анализа специфическое влияние, с которым иногда приходится считаться [31].

 

 

предыдущая                           оглавление                      следующая