§ 30. Спектры некоторых нестационарных процессов

 

Отличительным признаком нестационарного (в широком смысле) процесса является то, что его одно- и двумерные распределения или соответственно первый и второй моменты зависят от времени. Иначе говоря, нестационарность выражается в том, что среднее значение, либо дисперсия, либо функция корреляции являются функциями времени. Мы будем применять этот критерий в рассматриваемых ниже примерах.

В качестве первого примера рассмотрим случайный процесс, характеризующийся тем, что случайная величина принимает одно из двух равновероятных значений ±a; перемена знака может происходить только в фиксированные моменты

К описанному случайному процессу сводится, например, телеграфный сигнал при передаче равномерным кодом. На рис. 50 изображена одна из реализаций.

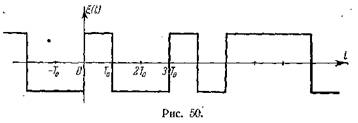
Составим выражение для распределения вероятностей. Одномерное распределение состоит из двух вероятностей

Выражение для одномерной плотности вероятностей можно записать с помощью дельта-функций

Одномерное распределение, как видим, от времени не зависит. Теперь рассмотрим распределение для  двумерной величины ξ, ξ_τ , представляющей собой совокупность двух значений случайного процесса, отстоящих друг от друга на т. Двумерное распределение, оказывается зависит, от времени. Именно, если

то моменты t и t + τ находятся внутри одного и того же интервала Т₀ и, следовательно, ξ и ξ_τ имеют одинаковый знак. (рис. 51)

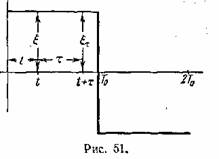
Таким образом,

Если же

то ξ и ξ_τ с равной вероятностью могут иметь любые знаки и, стало быть,

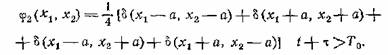
Таким образом, двумерная плотность вероятностей имеет на разных интервалах разные выражения, а это и значит, что она зависит не только от τ, но и от t. Итак, рассматриваемый процесс нестационарен.

Как указывалось выше, усреднение может производиться на любом этапе вычисления. Воспользовавшись этим, усреднением сразу по времени самое двумерное распределение.

Мы имеем

Перепишем неравенство

в виде

Усредняя распределение по интервалу Т₀ получим

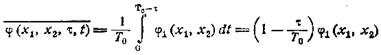
для τ, находящегося в интервале 0, Т₀. При

то есть при

получим, усредняя по интервалу T → ∞,

для τ в интервале Т₀ , . Итак, для усредненного распределения можем записать

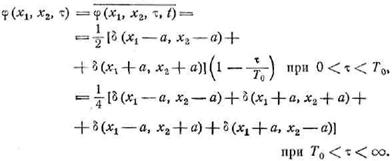
Подставляя усредненное распределение в формулу

найдем среднюю функцию корреляции

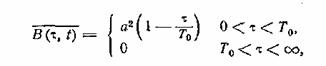
а затем и средний спектр

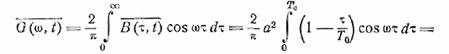
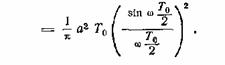                                                          (30.1)

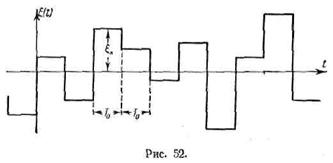
Для второго примера возьмем процесс несколько более общего вида: ось времени по-прежнему разбита на равные интервалы Т₀; в каждом интервале случайная величина принимает независимые значения ξ_κ, определяемые плотностью вероятностей φ(x) (рис. 52).

Для двумерной плотности вероятностей имеем следующие выражения:

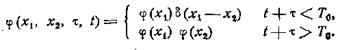
Если М(ξ) = 0, то после усреднения находим для функции корреляции и спектра

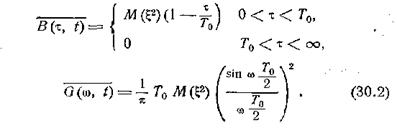
Рассмотренный процесс можно представить, как последовательность прямоугольных импульсов со скважностью единица, модулированных по амплитуде. Нужно заметить, что спектры различных видов импульсной модуляции удобнее находить, исходя из текущего спектра, подобно тому, как это было показано в § 28.

Рассмотрим общий случай амплитудно-импульсной модуляции. Процесс представляет собой последовательность импульсов произвольной формы f(t), модулированных по амплитуде, т.е. умноженных на случайный множитель ξ_κ (рис. 53).

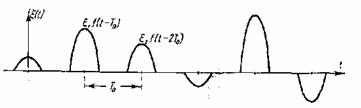
Рис. 53

Такой процесс может быть записан в виде

Составим выражение для текущего спектра

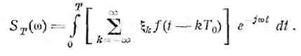
Переменим порядок действий с одновременной заменой пределов

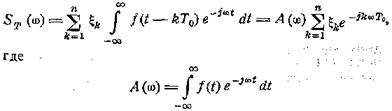
— спектр одиночного импульса, представляемого функцией f(t). Умножим S_T(ω) на сопряженную величину

Остается разделить на Т — пТ₀, перейти к пределу при T →  и взять среднее по множеству

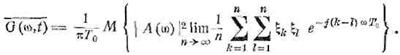
Мы будем иметь п членов, для которых k = l; после суммирования и деления на п эти члены дадут в среднем М(ξ²). Среднее значение произведения ξ_k ξ_l (в предположении, что ξ_k и ξ_l независимы) равно произведению средних, т.е. (М ξ)²; эта величина выходит из-под знака суммы. Вводя m = k — l, после преобразований, аналогичных проделанным в § 28, получим

(здесь слагаемое — (М ξ)² добавлено для того, чтобы сумма включала это слагаемое, соответствующее значению m = 0). Сумма в правой части представляет в виде ряда Фурье некоторую периодическую функцию частоты. Легко видеть, что эта функция есть не что иное, как последовательность дельта-функций вида

в чем можно убедиться, разложив функцию F(ω) в ряд Фурье. Функция F(ω) представляет собой линейчатый гармонический спектр; ω₀ =  ─ основная частота спектра, равная частоте следования импульсов. Таким образом G(ω) содержит сплошную и дискретную части; последняя отсутствует при Mξ = 0. Окончательное выражение для спектра записывается в виде

Применим эту формулу к процессу рис. 52, представляющему собой последовательность прямоугольных импульсов длительностью Т₀. В этом случае мы имеем

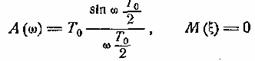
и, следовательно,

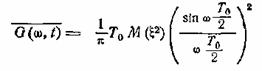
— результат, полученный ранее другим способом.

Разберем теперь случай импульсов, модулированных по фазе.

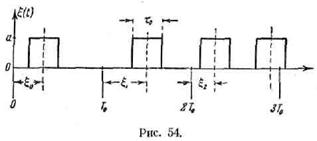
Процесс представляет собой последовательность импульсов одинаковой формы и величины, имеющих случайные смещения ε_к во времени относительно фиксированных равноотстоящих моментов kT_Q; иначе говоря, период cледования импульсов Т₀ получает случайные приращения ε_к. Величины ε_к предполагаются независимыми; процесс задается одномерным распределением φ(ε). На рис. 54 к примеру изображены прямоугольные импульсы. Мы не будем составлять выражения для двумерного распределения; заметим лишь, что произведение ξξ_τ, равно а^г при одновременном выполнении, двух условий

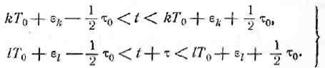
Если хотя бы одно из этих неравенств не соблюдается, то ξξ_τ = 0. Отсюда видно, что функция корреляции зависит не только от τ, но и от t, так что рассматриваемый процесс нестационарен.

Мы будем вычислять спектр непосредственно для импульсов произвольной формы. Процесс можно записать в виде

где f(t) — по-прежнему функция, представляющая отдельный импульс. Текущий спектр выражается, как

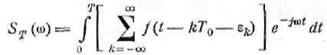
или, после перемены порядка действий и замены пределов,

где A(ω) — спектр одиночного импульса. Далее,

Усреднение по множеству дает

где

— характеристическая функция распределения ε. Преобразуя двойную сумму точно так же, как это делалось раньше, получим

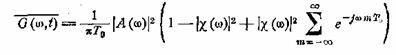
или

                   `              (30.4)

где

Перейдем теперь к исследованию синусоидальных колебаний, модулированных случайным процессом по амплитуде или по фазе.

Начнем с амплитудной модуляции, как более простой. Случайный процесс, спектр которого мы должны найти, записывается в виде

где ξ(t) — стационарный процесс. Составим произведение

Усреднив это произведение по множеству, получим

Сделаем теперь усреднение по времени; первый член в квадратных скобках выпадет, и мы будем иметь

Отсюда находим средний спектр

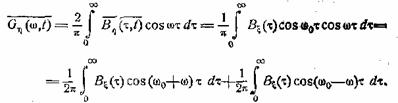
Итак,

                                       (30.5)

т.е. спектр модулированного колебания состоит из двух боковых полос, повторяющих спектр модулирующего процесса, и расположенных симметрично относительно несущей частоты ω₀. Таким образом, обычное строение спектра амплитудно-модулированного колебания сохраняется и в том случае, когда модулирующая функция есть случайный процесс.

Обратимся к фазовой модуляции. Здесь дело обстоит значительно сложнее [5].

Задача состоит в нахождении спектра случайного процесса вида

где θ₁(t) — случайный процесс. Но так как по смыслу фаза (аргумент косинуса) должна в среднем расти пропорционально времени, то мы будем рассматривать частный вид фазовой модуляции, выражаемый соотношением

                                                                                                                   (30.6)

Здесь θ(t) уже может быть стационарным процессом, что мы и будем предполагать.

Прежде всего нужно показать, что процесс (30.6) нестационарен. Для этого составим выражение для плотности вероятностей двумерной случайной величины ξ,ξ_τ. Мы имеем

                                               (30.7)

Плотность вероятностей для двумерной величины θ,θ_τ задана и равна φ_θ(υ₁,υ₂,τ). Искомая плотность φ_ξ(х₁,х₂,τ) должна быть выражена через φ₀. Дело сводится к замене переменных по известной формуле

где

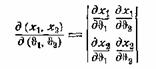
— якобиан преобразования. В нашем случае x₁ зависит только от υ₁, а х₂ — только от υ₂. Поэтому

и мы имеем:

Итак, плотность вероятностей φ_ξ зависит от времени, и процесс (30.6), следовательно, нестационарен.

Перейдем к вычислению спектра, для чего найдем предварительно функцию корреляции. Мы имеем

В нашем случае

Таким образом,

или, подставляя выражения х_х и х₂ через  и  из (30.7),

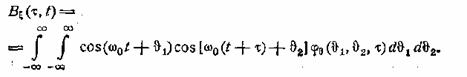
Преобразуя произведение косинусов, получим два члена, один из которых при усреднении по времени выпадает. Таким образом,

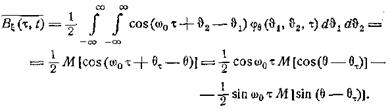
Мы ограничимся случаем симметричного распределения разности

В этом случае второй член выпадает, и мы получаем

Отсюда находим спектр процесса ξ(t)

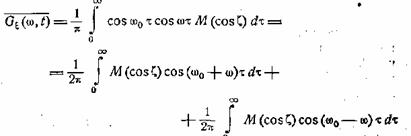
или

                                                    (30.8)

Итак, и в случае фазовой модуляции спектр состоит, как и следовало ожидать, из двух боковых полос. Спектр каждой из них выражается формулой

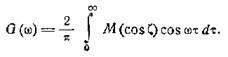                                                          (30.9)

Найдем среднее значение cos ζ. Пусть θ имеет нормальное распределение; в таком случае и разность

также имеет нормальное распределение, полностью определяемое дисперсией

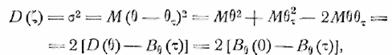
и мы можем теперь найти

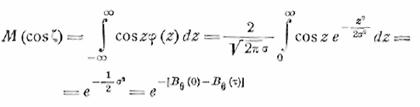
и выражение для спектра

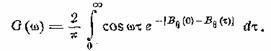                                        (30.10)

Эта формула выражает спектр фазово-модулированного колебания через функцию корреляции модулирующего процесса, распределение которого предполагается нормальным [1]. Чтобы довести вычисления до конца, мы рассмотрим частный случай; будем иметь в виду частотную модуляцию с большим индексом.

В случае частотной модуляции задается не непосредственно процесс θ(t), а процесс

выражающий мгновенное отклонение частоты от среднего значения ω₀. Таким образом, мы можем записать для частотно-модулированного колебания

Спектр процесса ξ(t) нужно выразить через характеристики процесса ν(t). Удобно воспользоваться преобразованием Фурье. Если

то

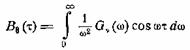
и входящая в предыдущие формулы величина σ может быть выражена через спектр мгновенного частотного отклонения G_ν(ω) следующим образом:

Пусть спектр G_ν равномерен и ограничен сверху частотою Ω, т.е.

.

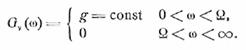
Тогда

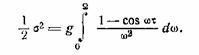
Для наших целей удобно представить этот интеграл в следующем виде:

где

Произведение

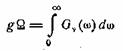
есть средний квадрат процесса ν(t), т.е. средний квадрат отклонения частоты от среднего значения. Обозначим эту величину через ∆ω². Введя обозначение индекса модуляции

можем переписать выражение для σ² в виде

Теперь перейдем к приближению для случая [5] большого индекса, т.е. для β » 1.

Случай большого индекса характеризуется тем, что в выражении для искомого спектра

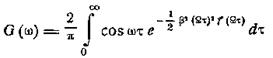
экспоненциальный множитель убывает тем быстрее, чем больше β. Это значит, что подынтегральное выражение становится пренебрежимо малым при тех меньших значениях τ, чем больше β. Следовательно, при большом β можно ограничиться малыми значениями τ. На этом и основано приближение. В частности, можно положить

с погрешностью, не превосходящей 0,01, если Ωτ ≤ 0,6. При этом условии будем иметь

если

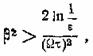
откуда, подставляя наибольшее значение Ωτ = 0,6 и выбирая ε = 0,01, найдем

β > 5.

Соображения, приводящие к описанному приближению, легко обобщаются на случай произвольного спектра G_ν модулирующего процесса ν(t) при условии, что ширина Ω спектра G_ν достаточно мала по сравнению со среднеквадратичным частотным отклонением ∆ω. Для получения этого более общего результата достаточно в выражении для σ² разложить 1 — cos ωτ в ряд и сохранить первый член ряда. Это даст

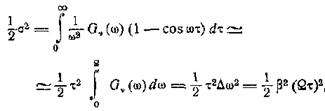
т.е. то же, что и раньше.

Итак, при большом индексе модуляции, или, что то же, при большом частотном отклонении, мы имеем для спектра приближенное выражение

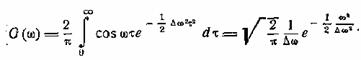                      (30. 11)

Здесь следует отметить, что при большом индексе спектр частотно-модулированного колебания не зависит от формы и ширины спектра модулирующего процесса; спектр определяется лишь частотным отклонением, причем ширина спектра частотно-модулированного колебания пропорциональна частотному отклонению.

 

 

предыдущая                           оглавление                      следующая