§ 29. Понятие спектра в применении к нестационарным процессам

 

В предыдущем мы занимались только эргодическими стационарными процессами. Но на практике приходится иметь дело и с процессами нестационарными, причем существенно, что такие процессы встречаются достаточно часто и имеют большое значение. К числу нестационарных процессов относятся многие виды сигналов связи. Так, например, обычное модулированное колебание

где ξ(t) — стационарный случайный процесс, является процессом нестационарным, что сразу видно хотя бы из того, что одномерное распределение пропорционально cos ωt, т.е. зависит от времени. При таком положении необходимо поставить вопрос о применимости спектральных представлений к некоторому интересующему нас классу нестационарных процессов. Дело сводится, конечно, к некоторому пересмотру и расширению определений, которыми мы до сих пор пользовались.

Как мы видели (см. § 27), вычисление спектра случайного процесса непременно связано с операцией усреднения. Для эргодических стационарных процессов средние по множеству и по времени с вероятностью единица равны друг другу. Поэтому безразлично, каким способом усреднения мы воспользуемся. Выбор усреднения определяется тем, как нам задан случайный процесс. В условиях эксперимента мы имеем дело обычно с отдельной реализацией случайного процесса; в этих условиях мы прибегаем к усреднению по времени. При теоретическом же исследовании случайный процесс задается распределением вероятностей, и в этом случае мы пользуемся усреднением по множеству.

Представим случайный процесс как функцию ξ(θ,t) двух переменных: случайного параметра θ и непрерывно текущего времени t. Зафиксировав некоторый момент t = t₀ , мы получим случайную величину ξ(θ,t₀), распределение которой в общем случае зависит от t₀. Закрепив же некоторое значение случайного параметра θ, мы получаем одну из возможных реализаций случайного процесса, представляющую собой уже неслучайную функцию времени.

Операция усреднения есть в сущности операция интегрирования с тем или иным весом. Так, среднее по времени находится из выражения

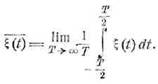
Среднее по множеству вычисляется, как

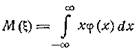
Но если мы имеем дело с функцией двух переменных, то, в общем случае, усреднение по одной переменной даст величину, зависящую от второй переменной, и наоборот. Применительно к случайным процессам это значит, что среднее по множеству, в общем случае, зависит от времени, а средние по времени образуют случайное множество. Эргодический стационарный процесс тем и замечателен, что для него средние по времени и по множеству равны друг другу, а из этого непосредственно следует, что они не зависят от второй переменной (так как функции разных аргументов могут быть равны друг другу только в том случае, когда эти функции представляют собой постоянные, т.е. величины, не зависящие от аргументов).

Таким образом, среднее для нестационарного процесса, рассматриваемого как функция двух переменных, может определяться как результат двукратного усреднения — по множеству и по времени. Порядок усреднения безразличен, так как дело сводится всего лишь к изменению порядка интегрирования. Так, произведя для нестационарного процесса усреднение по множеству, мы получим величину, зависящую от времени; для устранения этой зависимости следует произвести повторное усреднение, на этот раз по времени. Усредняя сперва по времени, получим случайное множество; требуется дополнительная операция усреднения по этому множеству.

Для полноты картины следовало бы разобрать вопрос о том, для какого класса нестационарных процессов среднее в указанном смысле, во-первых, существует, а во-вторых, не лишается того физического смысла, который мы обычно усредняемой величине приписываем. Не предпринимая здесь такого исследования, заметим лишь, что в качестве примеров в дальнейшем рассматриваются только такие нестационарные процессы, для которых функция корреляции и спектр, вычисленные путем двойного усреднения, сохраняют свой обычный смысл [1]. Во избежание недоразумений мы будем называть функцию корреляции и спектр нестационарных процессов, полученные двукратным усреднением, средней функцией корреляции и средним спектром.

Покажем теперь, что средние функция корреляции и спектр по-прежнему связаны между собой парой преобразования Фурье. В качестве исходных возьмем следующие два определения:

Запишем выражение для текущего спектра

и умножим на сопряженную величину

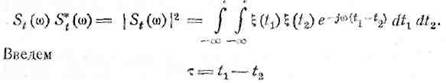
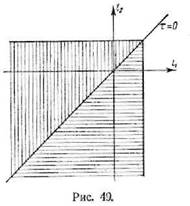
и разобьем область интегрирования на две, как показано на рис. 49. Это даст

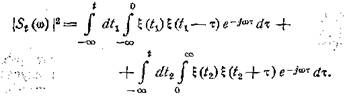
Усредним обе части этого равенства по множеству, замечая, что

Мы получим

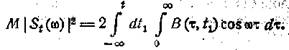
Дифференцируя по t и подставляя результат в исходное определение спектра, находим

Отсюда усреднением по времени получаем связь между средним спектром и средней функцией корреляции

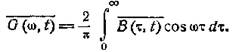
Справедливо и обратное преобразование

(сравни с формулами (27.11) и (27.12)).

Вывод из всего сказанного состоит в том, что мы можем воспользоваться для вычисления функций корреляции и спектров нестационарных процессов формулами, приведенными в § 27, добавив в них второе усреднение. С точки зрения вычислений существенно, что это второе усреднение может производиться на любом этапе вычисления, как показано на примерах следующего параграфа.

 

 

предыдущая                           оглавление                      следующая