§ 25.
Динамическая характеристика резонатора при воздействии
изменяющейся частоты
В
предыдущем параграфе был рассмотрен вопрос о динамической разрешающей способности резонатора в
системе одновременного анализа.
Теперь
мы разберем соотношения при последовательном анализе, т.е. в случае, когда изменяется
возбуждающая резонатор частота.
При воздействии на резонатор
изменяющейся во времени частоты наблюдаются
резонансные явления. Однако, если изменение частоты происходит достаточно
быстро, то наиболее интенсивные колебания происходят не в тот момент,
когда возбуждающая частота совпадает с резонансной, а несколько позже, так как
резонатор не успевает раскачаться; по этой же причине и наибольшая амплитуда
колебаний оказывается меньше, чем при резонансе в установившемся режиме. Если
построить график зависимости амплитуды колебаний от мгновенной частоты, то
получится динамическая резонансная кривая. Эта кривая при быстром изменении
частоты может существенно отличаться от статической резонансной кривой, а
именно: 1) положение максимума смещается по шкале частот (что соответствует
смещению по шкале времен в сторону запаздывания); 2) высота максимума убывает;
3) кривая становится асимметричной — левый скат делается более пологим; 4)
полоса пропускания возрастает (т.е. разрешающая способность убывает); 5)
явление осложняется еще убыстряющимися колебаниями
амплитуды, обусловленными биениями между вынужденными колебаниями и
собственными колебаниями, возникшими при прохождении через резонанс. Все
эти особенности видны на рис. 40, на котором представлены статическая (а) и
динамическая (б) резонансные кривые.
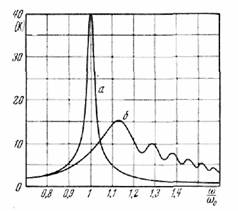
Рис. 40.
Теория явления была
предметом многочисленных исследований [4, 7, 19, 23, 26]. Нижеследующее
изложение основывается на работах Турбовича [15, 16], дающих достаточно
общий подход к проблеме, и в то же время позволяющих получить ответ на
вопросы, вытекающие из потребностей практики.
Пусть частота
изменяется со временем по линейному закону
Ω
= ω1 + λt. (t
> 0)
Напряжение, воздействующее на резонатор, можно записать
в комплексной форме
,
где
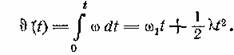
Выходное напряжение представим интегралом Дюамеля
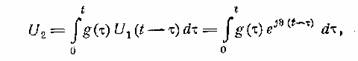
где g(x) — импульсная реакция резонатора.
Подставляя значение 
, находим
Но
и, таким образом,
Динамический коэффициент
передачи определим как отношение комплексных напряжений U2 и U1
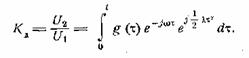(25.1)
Это — точная формула, имеющая достаточно универсальный
характер, так как она годится для любого резонатора.
Перейдем теперь к
приближениям. Прежде всего заметим, что g(t) есть функция, содержащая экспоненциально-убывающие
множители. Поэтому, с незначительной погрешностью (которая оценивается ниже)
можно заменить верхний предел на бесконечность:
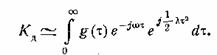(25.2)
При λ
→ 0, т.е. при переходе к статическому режиму, получим известное выражение
для статического коэффициента передачи, как преобразования Фурье импульсной
реакции
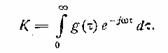(25.3)
Таким образом, разность между динамическими
коэффициентами передачи равна
(25.4)
Далее
отметим, что нас интересует случай, когда динамическая резонансная кривая мало
отличается от статической, так как только при этом условии погрешность
анализатора, рассчитанного по статическим параметрам, будет мала. Полагая аргумент λτ2
малым для всех значений τ,
для которых убывающая функция g(τ)
имеет еще заметную величину, можем разложить выражение в круглых скобках под
знаком интеграла в (25.4) в степенной ряд и ограничиться для первого
приближения всего двумя членами разложения. Это даст
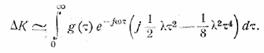
Теперь заметим, что появление
множителей хn можно представить как результат n-кратного дифференцирования
по параметру ω.
Следовательно,
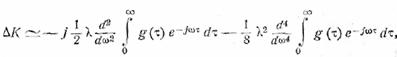
то есть
Итак, для динамического коэффициента передачи имеем
(25.5)
Полагая
можем составить общее выражение для квадрата модуля
динамического коэффициента передачи
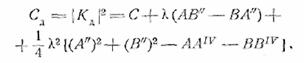(25.6)
Приближенные формулы (25.5) и
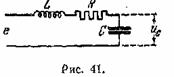
(25.6) имеют общий характер. В дальнейшем мы будем рассматривать только
простейший резонатор по схеме рис. 41, для которого
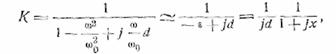
где
— обобщенная расстройка. С точностью до постоянного
множителя
и этим выражением мы и воспользуемся в дальнейшем.
Поставим задачу дальнейшего исследования. Имея в виду
практические вопросы расчета и построения анализаторов (а также характерографов
и других приборов, использующих модулированное по частоте испытательное
напряжение), мы должны, очевидно, выяснить, как зависят те или иные параметры,
определяющие резонансную кривую, от скорости изменения частоты. В частности,
нас интересует: 1) смещение максимума — s, 2)
уменьшение высоты максимума — ∆С, 3) смещение полосы пропускания —
½(s1 + s2), 4) изменение ширины полосы пропускания —s2 — s1. Смысл введенных здесь обозначений поясняется рис. 42, на
котором по-прежнему а — статическая, б — динамическая резонансные кривые.
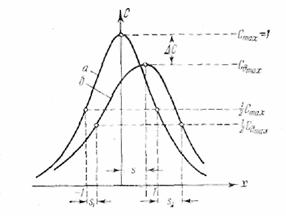
Рис. 42.
Для определения перечисленных
величин будем исходить из выражения (25.5) для динамического коэффициента
передачи, переписав его в новых переменных:
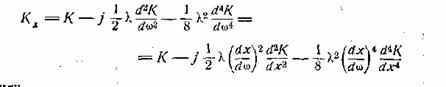
Или
(25.8)
где
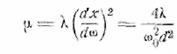
В формуле (25.8) К = К(х) и
производные берутся по аргументу х. Для модуля динамического
коэффициента передачи находим
(25.9)
Максимум статического коэффициента передачи
достигается при х = 0
Сmax=(0)=1; С'(0)
= 0.
Максимум динамического
коэффициента передачи имеет место при
некотором значении х — s, которое и является искомым. Разложим С´д в ряд Маклорена, ограничившись членом
первого порядка:
Подставляя сюда значение Сд из (25.9) и сохраняя лишь члены до
µ, получим уравнение
относительно s; решение этого уравнения есть
s = 2µ (25.10)
т.е. смещение максимума при динамическом резонансе
имеет тот же порядок малости, что и параметр µ, пропорциональный скорости изменения частоты.
Для нахождения относительного
изменения высоты максимума составим выражение
Подставляя сюда Сд и s из (25.9) и (25.10), найдем с точностью до µ².
∆С = — µ²
. (25.11)
Таким образом, изменение высоты максимума имеет второй
порядок малости относительно µ.
Определим теперь
значения обобщенной расстройки х, при которых квадрат модуля
коэффициента передачи равен половине максимального значения (в соответствии с
обычным определением ширины полосы пропускания). Для статического коэффициента
передачи
Для динамического коэффициента передачи
Разложив это выражение в ряд по искомым малым
параметрам s1 и s2 (с точностью до µ²),
получим уравнения для определения этих величин. Разность s2 — s1 дает
приращение относительной ширины полосы пропускания; вычисление дает
(25.12)
Расширение полосы пропускания имеет, как видим, второй
порядок малости относительно µ. Центр
полосы пропускания для динамической резонансной кривой смещен относительно х
= 0 на величину полусуммы s1 и s2. Вычисление дает
½(s1 + s2) = µ (25.13)
Сравнивая (25.13) и (25.10), замечаем, что смещение
центра полосы вдвое меньше смещения максимума. Это обусловлено уже
упоминавшейся ассимметрией динамической резонансной кривой.
Итак, одночленные
выражения первого приближения для рассмотренных параметров динамической
резонансной кривой пропорциональны µ
или µ², т.е. имеют первый
или второй порядок малости, если µ — величина
первого порядка малости. Грубое искажение резонансной кривой, показанное на
рис. 42, едва ли встретится в практике построения радио-измерительных
устройств; динамическая резонансная кривая рис. 42 относится к значению µ 
30 (d =
0,025).
Вернемся от обобщенных переменных к исходным. Обозначим через ∆ω ширину полосы пропускания; знаком δ обозначим приращения, получаемые
теми или иными параметрами в динамическом режиме. Тогда вместо формул (25.10), (25.11) и (25.12) будем иметь
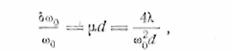(25.10´)
(25.11´)
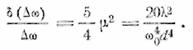(25.12´)
Необходимое время
анализа (или период частотной модуляции при пилообразном законе модуляции)
может быть определено по формуле
где F — размах
модуляции, т.е. ширина обследуемого диапазона частот, ∆ƒ — разрешающая
способность, т.е. ширина полосы пропускания (при выводе этой формулы положено 
)
Так, например, для
гетеродинного анализатора звуковой частоты (F =
10 кгц) с электромеханическим резонатором, настроенным на частоту 50 кгц,
при разрешающей способности 25 гц (что соответствует d = 5 • 10 ─4),
задаваясь µ = 0,1 (т.е. допуская
расширение полосы на величину порядка 1%), получим
На практике считают
достаточным ставить менее жесткие требования: полагают µ ≤ 1. При µ порядка единицы
вышеприведенные приближенные формулы, разумеется, уже неприменимы.
Вернемся к исходному выражению
(25.1) для динамического коэффициента передачи. Мы заменили в этом выражении
верхний предел на бесконечность (см. (25.2)), полагая, что вносимая этой
заменой погрешность невелика. Нам нужно теперь оцепить
величину погрешности равной
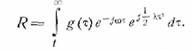
Модуль интеграла меньше интеграла от модуля; поэтому
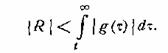
Подставляя
запишем
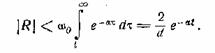
Но
и, стало быть,
Относительную погрешность получим, отнеся R к
Кmах = 1/jd
Все расчеты велись с точностью до µ². Для того чтобы относительной погрешностью можно было
пренебречь, достаточно, чтобы она имела
следующий порядок малости, т.е. порядок µ³. Отбрасывая не влияющий на порядок множитель 2, будем иметь
или, после логарифмирования
Смысл этого неравенства
состоит в том, что для получения достаточно точных результатов в полосе частот,
начиная с обобщенной расстройки х, нужно, чтобы начальная частота,
соответствующая значению х, была достаточно удалена от границы
исследуемой полосы. Пусть, например, µ = 0,1. Тогда
x ─ х1 ≥
3∙0,1∙ln 10 = 0,69.
Напомним, что ширина полосы пропускания простого
резонатора, выраженная через обобщенную расстройку, равна 2. Таким образом,
нужно отступить влево от края исследуемой полосы всего лишь на долю полосы
пропускания резонатора, для того чтобы иметь право пренебречь погрешностью R при
переходе от (25.1) к (25.2). Это условие, конечно, на практике всегда
выполняется, и все соотношения, выведенные на основании формулы (25.2) таким
образом, подтверждены.
Предыдущее изложение
основывалось на предположении малости отличия динамической частотной
характеристики от статической; считалось само собою
разумеющимся, что мы должны стремиться к такому положению. Это справедливо,
если мы рассчитываем анализатор на основе параметров статической характеристики резонатора. В этом случае различие между статической и динамической
характеристиками рассматривается как источник погрешности, и желательно,
разумеется, чтобы эта погрешность была мала. Но возможен и иной подход к
вопросу. Именно, если скорость изменения
частоты постоянна, то анализатор может рассчитываться на основе параметров динамической характеристики. В этом случае скорость изменения частоты может
быть как угодно велика, если только значения динамических параметров (например,
ширина полосы пропускания) нас устраивают.
В
заключение интересно заметить, что вопрос о явлениях, возникающих при воздействии изменяющейся частоты
на резонансную систему представляет интерес и для других отраслей
техники. Так, при пуске машин с
неуравновешенными вращающимися массами на
гибком валу, могут возникать опасные колебания при прохождении через
резонанс (так называемая «критическая скорость»). Математическая формулировка
задачи в точности совпадает с нашей [7,26]. Однако
цель расчета противоположна: нужно подобрать безопасный режим пуска, т.е.
обеспечить настолько быстрое изменение скорости вращения, чтобы, так сказать,
«проскочить» через резонанс, не возбудив на критической скорости колебаний
чрезмерной амплитуды. В наших обозначениях это значит, что нужно, задаваясь допустимым наибольшим значением Kдmax
, выбрать наименьшее значение µ » 1.
предыдущая оглавление следующая
