§ 22. Действительные условия работы анализатора

 

Выводы § 19 требуют серьезных коррективов с точки зрения действительных условий работы анализатора, которые мы и постараемся сейчас разобрать.

В самом начале отмечалось, что периодическая функция вида

ƒ(t) = ƒ(t + nT)

есть математическая абстракция. Но если бы даже существовало явление, отвечающее этому определению, то оно не существовало бы для анализатора. Ведь анализатор в действительности включается на конечное время, и, следовательно, анализируемое явление для анализатора представляется отрезком на протяжении от момента включения до момента выключения.

Анализатор может дать истинный спектр явления в том единственном случае, когда анализируемое явление полностью укладывается в этот отрезок времени, т.е. когда анализируется заведомо непериодическое явление типа импульса, равного нулю вне конечного промежутка времени, и при условии, что этот промежуток времени, т.е. длительность импульса, меньше времени включения анализатора. При анализе же длительных явлений, периодических или непериодических, анализатор принципиально не в состоянии дать истинный, спектр этих явлений. По определению спектр выражается интегралом

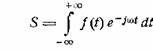                                                                                                                         (22.1)

Если анализатор выполняет требуемое умножение и интегрирование, то он во всяком случае не может произвести интегрирование в бесконечных пределах. Анализатор «не знает», что происходило до его включения, и тем более «не знает», что будет происходить после его выключения. Он может лишь произвести интегрирование на промежутке t₁ < t <t₂, где t₁ и t₂ — соответственно моменты включения и выключения.

В лучшем случае можно ожидать от анализатора, что он, действуя непрерывно, выполняет интегрирование на промежутке от момента включения до текущего момента. Если принять момент включения за начало отсчета времени, то анализатор может измерить величину

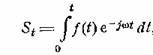                                                                                                                          (22.2)

т.е. текущий спектр функции f(t) (см. § 5). Чем больше время включения, тем больше текущей спектр приближается к истинному спектру длительного явления. Если время включения очень мало, то каков бы ни был характер явления, анализатор получает лишь короткий импульс, сплошной спектр которого имеет однородную плотность вплоть до частот, определяемых временем включения, и тем более высоких, чем время включения меньше, т.е. чем импульс короче.

Эти соображения легко проверить экспериментально. Синусоидальное колебание воспринимается слухом как чистый музыкальный тон. Если включать этот тон на все более короткие промежутки времени, то ясное ощущение высоты тона будет постепенно утрачиваться, пока, наконец, достаточно кратковременное включение не будет восприниматься просто как щелчок — это и соответствует короткому импульсу с широким сплошным спектром.

Из всего сказанного следует, что результат анализа принципиально зависит от времени. Учесть эту зависимость можно, опираясь на две различные (но приводящие, конечно, к одним и. тем же выводам) точки зрения: временную и спектральную (частотную).

Приведем подробное рассуждение о процессе анализа с обеих точек зрения.

а. Временная точка зрения. Мы исходили в предыдущем при определении разрешающей способности резонатора из его резонансной кривой (частотной характеристики). Но резонансная кривая представляет поведение резонатора в установившемся режиме. Установившимся режимом мы называем режим, достигаемый по окончании переходных явлений, возникающих при включении, т.е. теоретически через бесконечно большое время. Практически переходными явлениями можно пренебречь уже по прошествии конечного времени. Однако время установления тем больше, чем больше избирательность резонатора, т.е. чем меньше его затухание. А в применении к анализу нас интересуют именно резонаторы с высокой избирательностью. Стало быть, исследуя работу анализатора, мы не можем, вообще говоря, игнорировать переходные явления. Составляя и решая соответствующие дифференциальные уравнения, мы получим амплитуду колебаний резонатора как функцию не только, частоты (как в установившемся режиме), но и времени. Следовательно, резонансная кривая резонатора будет различной для различных моментов времени; ее уместно назвать динамической резонансной кривой в противопоставление обычной резонансной кривой, которую мы будем называть статической и которая является предельной формой динамической резонансной кривой при t → ∞.

Таким образом, все ранее выведенные соотношения сохраняют смысл лишь в качестве предельных. Истинная разрешающая способность анализатора определяется его динамической резонансной кривой. Ее максимум тем тупее, чем меньше время включения; следовательно, анализ выполняется тем точнее, чем больше время анализа.

б. Спектральная точка зрения. Мы исходили в предыдущем при определении разрешающей способности анализатора из представления, что на анализатор воздействует периодическое, в частности, синусоидальное колебание. В действительности этого нет: анализатор включается лишь на конечное время. Следовательно, для каждого данного момента воздействие на резонатор может быть представлено непериодическим явлением, а именно отрезком синусоиды, длящимся от момента включения до текущего момента. Анализатор будет анализировать это явление с присущей ему статической разрешающей способностью. Но так как спектр самого воздействия с течением времени изменяется («текущий спектр»), то будет изменяться и показание анализатора. В частности, при анализе синусоиды в самые первые моменты, когда периодический характер явления еще не определился и текущий спектр практически однороден, анализатор даст почти одинаковые показания на всех частотах. Лишь в пределе, когда сплошной текущий спектр выродится в дискретную спектральную линию, анализатор даст спектр, определяемый на основе стационарных представлений, изложенных выше. Эти представления сохраняют, таким образом, силу при выводе предельных соотношений. В действительности же показание анализатора оказывается тем более размытым, т.е. разрешающая способность его тем меньше, чем меньше время включения.

Обе точки зрения — временная и спектральная — теоретически равноценны. В дальнейшем использована временная точка зрения и вот по каким методическим соображениям:

1. Временная точка зрения представляется легче усвояемой и менее формальной.

2.  Стоя на временной точке зрения, мы можем характеризовать анализатор как таковой независимо от режима его включения и характера анализируемого явления[1].

3.  Некоторые вопросы вообще затруднительно (хотя и возможно в принципе) излагать на спектральном языке. В частности, здесь имеется в виду вопрос о последовательном анализе. Все предыдущее относилось к одновременному анализу, когда речь идет об отклике на то или иное воздействие резонатора с постоянной настройкой. Но если обратиться к анализатору, содержащему резонатор с переменной настройкой, то мы имеем дело с явлениями более сложными, и оказывается более удобным говорить о них на временном языке.

И в случае последовательного анализа очевидно, что свойства резонатора могут описываться статической резонансной кривой лишь при бесконечно медленной перестройке. В действительности анализ происходит с конечной скоростью. Легко понять, что чем быстрее настройка резонатора проходит через частоту данной спектральной составляющей, тем в меньшей степени эта составляющая успеет раскачать резонатор. То же относится и к варианту с применением вспомогательной частоты, когда настройка резонатора неизменна, а спектр исследуемого колебания передвигается с той или иной скоростью по шкале частот.

В случае последовательного анализа свойства анализатора также могут с удобством описываться посредством динамической резонансной кривой. Теория и опыт показывают, что ее максимум тупее, чем у статической резонансной кривой, причем тем тупее, чем больше скорость относительного движения по шкале частот настройки резонатора и исследуемого спектра, т.е. чем больше скорость анализа. Таким образом, и в этом случае разрешающая способность тем меньше, чем больше скорость анализа.

Из всего сказанного следует, что понятие разрешающей способности анализатора лишено практического смысла, если оно не связано так или иначе со скоростью (или продолжительностью) анализа. Очевидно, что для полной характеристики свойств анализатора мы должны ввести понятие динамической разрешающей способности анализатора, зависящей как от параметров анализатора, так и от скорости анализа. Последующие параграфы посвящены подробному исследованию этого вопроса, причем одновременный и последовательный анализы рассмотрены порознь, так как постановка вопроса в этих двух случаях довольно существенно различается.

 

 

предыдущая                           оглавление                      следующая