§ 20. Об
анализе без резонаторов
До сих пор предполагалось, что
анализ выполняется при помощи резонатора, т.е. некоторого устройства,
обладающего определенной частотной избирательностью. Простейшим резонатором
является колебательный контур; более совершенным избирательным органом может
служить полосовой фильтр.
Существует, однако, и другая возможность,
которую мы рассмотрим в общих чертах. Составим схему, показанную в скелетной
форме на рис. 33.
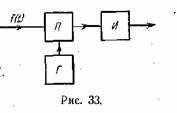
На этой схеме П
— перемножитель (идеальный модулятор), т.е.
устройство, на выходе которого получается напряжение, пропорциональное
произведению напряжений, поданных на два входа: Г — генератор
синусоидального напряжения с изменяемой частотой и начальной фазой, И —
интегрирующая схема. Если генератор дает напряжение
U = cos ωt,
то на выходе мы получим
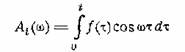
(предполагая, что схема включена в момент t = 0). Если изменить начальную фазу напряжения
генератора на π/2, то на выходе будем иметь
![]()
Величины At и
Bt представляют
собой косинусную и синусную составляющие текущего спектра. Соединив вместе две
схемы рис. 33 с двумя генераторами, дающими сдвинутые на π/2
синусоидальные напряжения, и добавив звено, в котором At и
Bt возводятся
в квадрат и складываются с последующим извлечением корня, получим анализатор,
на выходе которого получается текущий амплитудный спектр функции f(t)
![]()
Можно видоизменить
описанный метод получения спектра так, чтобы можно было обойтись одной схемой
рис. 33. Для этого нужно при данной частоте ω изменять фазу φ напряжения
генератора. Тогда на выходе схемы рис. 33 будем иметь
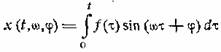
Найдем наибольшее
значение х, считая фазу φ переменной.
Для этого приравняем нулю производную ![]()
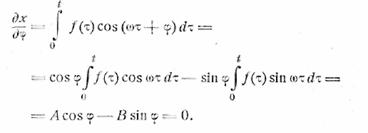
Отсюда
![]()
Подставляя эти значения в выражение для х, получим
![]()
Итак, если подбором фазы
добиться максимума (при данной частоте) выходного напряжения схемы рис. 33, то
получим непосредственно амплитудный спектр (модуль комплексного спектра). Вышеописанная
схема действует в полном соответствии с математическим определением спектра,
выполняя все операции, входящие в это определение; короче говоря, схема рис. 33
выполняет преобразование Фурье. Следовательно, эта схема является идеальным
анализатором, обладающим бесконечной разрешающей способностью.
Но теперь нужно
заметить, что схема обладает свойствами идеального анализатора лишь поскольку ее составные части идеальным образом
выполняют свое назначение, мы предполагали,
что перемножитель идеально перемножает, интегратор
идеально интегрирует, а генератор дает безукоризненное синусоидальное
напряжение. В действительной схеме все эти условия, разумеется, в той или иной
мере нарушены.
Мы рассмотрим теперь схему, в
которой одно из идеальных звеньев заменено реальным, а именно: вместо
идеального интегратора И включим в схему
рис. 33 простейшую интегрирующую схему в виде RС-звена
(рис. 34).
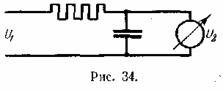
Положим, для простоты, что
анализируемое напряжение чисто синусоидально, и что мы рассматриваем
установившийся режим анализатора. Для установившегося режима коэффициент
передачи интегрирующей схемы рис. 34 равен
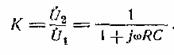
Напряжение, подаваемое
на вход интегрирующей схемы, равно произведению анализируемого напряжения и
напряжения генератора (пусть начальные фазы обоих напряжений совпадают):
![]()
Для комплексных амплитуд
напряжения на выходе можем записать
![]()
При ω, мало
отличающейся от Ω, первой величиной можно пренебречь, и мы получим
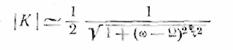
или
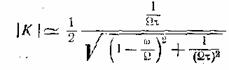 ,
,
где
τ = RC
— постоянная времени
интегрирующей схемы.
Полученное
выражение только постоянным множителем 1/Ωτ отличается от
выражения для коэффициента передачи простого колебательного контура: 
Таким образом, оказывается,
что рассматриваемая нами схема анализатора обладает совершенно такими же
свойствами в отношении избирательности, как и обычный резонатор, и,
следовательно, к ней применимо все то, что говорилось ранее о разрешающей
способности и погрешности анализатора с резонаторами.
Интересно,
что в рассматриваемом анализаторе роль затухания играет величина 1/Ωτ. Так
как для увеличения постоянной времени τ = RC нет практических
ограничений, то можно получить анализатор с очень высокой разрешающей
способностью. С другой стороны,
разрешающую способность можно легко и в широких пределах изменять
путем изменения R или С. Используя это, можно, например,
исследовать тонкие детали какого-либо участка спектра.
Техническое выполнение
описанной системы возможно в самых различных формах. В качестве поучительного
примера приведем предложенное в свое время применение в качестве анализатора
обычного ваттметра. В частности, если взять электродинамический прибор, то для
использования его в качестве анализатора достаточно подать анализируемое
напряжение и напряжение от генератора соответственно на две обмотки прибора
(статора и ротора). Вращающий момент пропорционален произведению токов в
обмотках; таким образом осуществляется перемножение.
Интегрирование выполняется в механической части прибора (за счет баллистических
свойств ротора). Если желательно перемножать непосредственно напряжения (а не
пропорциональные им токи), то вместо электродинамического ваттметра можно взять
квадрантный электрометр. Отсчет в такого рода устройствах
берется обычно не по постоянному отклонению (при нулевой разностной частоте), а
по амплитуде колебаний подвижной части прибора на низкой частоте ω0 ее
механического резонанса. Опишем происходящие при этом явления. Если
вспомогательная частота ω
медленно изменяется, проходя через значение Ω,
то на прибор воздействует переменная разностная частота │Ω — ω│, которая сначала
убывает до нуля, а затем снова возрастает. При этом подвижная система прибора
колеблется, амплитуда колебания имеет два максимума, когда разностная частота
сравнивается с собственной частотой подвижной системы. Процесс,
происходящий в измерительном приборе при медленном изменении ω), показан
на рис. 35.
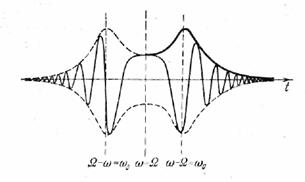
Рис. 35.
Амплитуда сначала мала, затем нарастает до максимума,
затем убывает до некоторого постоянного отклонения; затем все происходит в
обратном порядке. Огибающая процесса есть не что иное, как резонансная кривая
подвижной системы прибора. С точки зрения основного принципа анализатора мы
должны были бы взять отсчет при ω = Ω, когда стрелка остановится. Но практически гораздо удобнее
взять отсчет в точках, где подвижная система резонирует.
В заключение нужно дать ответ на
естественно возникающий вопрос: существует ли принципиальная разница между
анализом при помощи резонаторов и анализом по вышеописанному методу?
Разница, конечно, существует, и имеет
принципиальный характер. Это та же разница, какая имеется между фильтрацией и гетеродинированием. Описанный метод есть в сущности метод
преобразования частоты, или, в частности, метод синхронного детектирования по
отношению к той или иной составляющей спектра. Принципиальный характер различия
состоит в том, что фильтрация осуществляется посредством пассивной линейной
системы с постоянными параметрами, тогда как рассмотренный гетеродинный
анализатор с физико-математической точки зрения сводится к некоторой линейной
системе с переменными параметрами.
предыдущая оглавление следующая