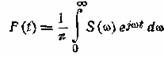§ 8. Перенос спектра

 

Для техники представляет большой интерес вопрос о возможности такого преобразования заданной функции времени, в результате которого спектр функции переместился бы по шкале частот. При обычной модуляции или преобразовании частоты получаются, как известно, две боковые полосы. Спрашивается, каким образом можно получить спектр, состоящий только из одной боковой полосы (ОБП)? Требуемое преобразование спектра показано на рис. 11.

 

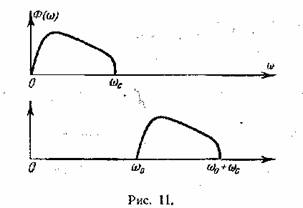
Мы полагаем, что исходный спектр ограничен сверху частотой ω₀.

Нужно сразу пояснить, что теорема смещения (§4) не дает требуемого преобразования, так как она относится к смещению комплексного спектра S(ω), тогда как нам требуется сместить вещественный спектр амплитуд Φ(ω) = │S(ω)│.(см. [9]).

Простейший способ получения смещенного спектра состоит в том, что сначала посредством балансной модуляции несущей частоты образуют двухполосный модуляционный спектр, а затем при помощи фильтров подавляют нижнюю боковую полосу. Представляют интерес и другие возможности, две из которых мы здесь рассмотрим. Будем исходить из выражения (2.14)

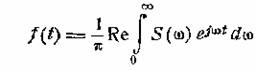                                                                                                       (8.1)

Нам нужно построить функцию, которая имела бы спектральную плотность на частоте ω₀ + ω. Для такой функции можем записать

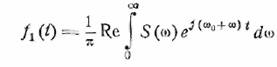                                                                                                (8.2)

Это выражение можно преобразовать следующим образом:

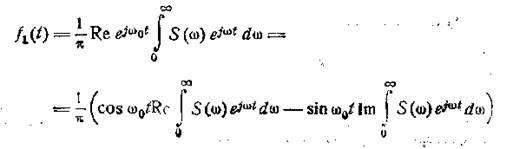
или

                             ƒ₁(t) = ƒ(t) cos ω₀t + ƒ(t) sin ω₀t [1]                                                                   (8.3)

Определим функцию

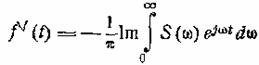                                                                                                       (8.4)

Для этого представим комплексный спектр в виде

Подставляя в (8.4), получим

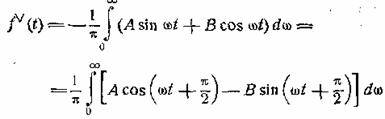                ,                        (8.5)

тогда как для функции ƒ(t) аналогичным путем получаем

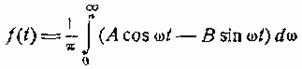                                                                        .        (8.6)

Сопоставляя (8.5) и (8.6), видим, что функция ƒ(t) отличается от ƒ(t) тем, что все составляющие повернуты по фазе на π/2. Следовательно, для образования функции ƒ(t), нужно располагать фазовращателем, поворачивающим фазу на π/2 для всех частот, т.е. четырехполюсником, комплексный коэффициент передачи которого равен

                                                                                                                 (8.7)

Четырехполюсник с такими свойствами физически неосуществим; можно, однако, построить реальный четырехполюсник, в котором характеристика (8.7) осуществляется с тем или иным приближением в конечном интервале частот (исключая ω = 0 и ближайшую окрестность этого значения). Требуемое преобразование (8.3) выполняется скелетной схемой рис. 12,

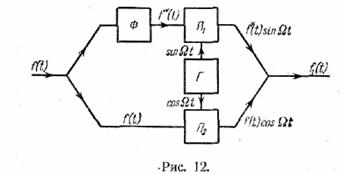
на которой: Φ — фазовращатель, поворачивающий фазу на π/2; Г—двухфазный генератор, дающий два сдвинутых на π/2 колебания: sin ω₀t и cos ω₀t; П₁ и П₂ —перемножители (балансные модуляторы).

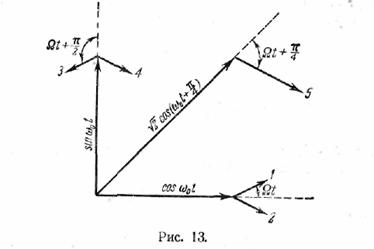
Сущность преобразования (8.3) поясняется векторной диаграммой рис. 13, на которой представлен случай

Для наглядности принята не балансная, а обычная AM, так что составляющая несущей частоты ω₀ не уничтожается. По горизонтали отложен вектор несущего колебания cos ω₀t; в результате модуляции функцией ƒ(t) появляются два спутника, представленные векторами 1 и 2, расположенными под углом ± Ωt по отношению к основному вектору. По вертикали отложен вектор sin ω₀t; модуляция функцией ƒ(t) дает два спутника, векторы которых 3 и 4 расположены под углом  к основному. Направления векторов 2 и 4 совпадают, а направления векторов 1 и 3 — противоположны. В результате сложения получается вектор несущей частоты и один единственный спутник — вектор 5. Второй спутник устраняется, и это и есть однополосная синусоидальная модуляция [2].

Можно показать, что рассмотренное преобразование есть частный случай многофазной модуляции, так что описанный механизм можно назвать двухфазной однополосной модуляцией. С технической точки зрения больший интерес представляет трехфазная однополосная модуляция [17].

Рассмотрим теперь другую возможность переноса спектра. Спектр, ограниченный сверху частотой ω₀, может быть представлен рядом Фурье (см. § 14):

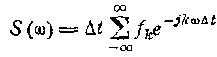                                                                                                                     (8.8)

где

                              

Спектр S(ω), сдвинутый на ω₀ по шкале частот, связан с исходным спектром S(ω) соотношением

S₁(ω₀ + ω) = S(ω)

так что

                                                                                          (8.9)

Соответствующая этому спектру функция времени выражается соотношением

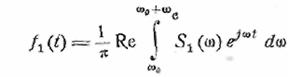                                                                             (8.10)

Подставляя сюда выражение (8.8) для спектра, находим [8,9]

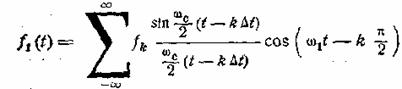                            ,   (8.11)

где

— центральная частота перенесенного спектра. Для исходной функции ƒ(t) (спектр которой выражается формулой (8.8)) имеем

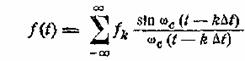                                                                                           (8.12)

Рассмотрение формулы (8.11) указывает характер преобразования, которому нужно подвергнуть исходную функцию ƒ(t),

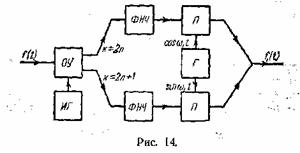
чтобы получить функцию ƒ₁(t) со смещенным спектром. Такое преобразование может быть выполнено скелетной схемой рис. 14. На этой схеме: ИГ—импульсный генератор с периодом следования ∆t; ОУ — отсчетное устройство, назначение которого состоит в том, чтобы в моменты, задаваемые импульсами, поступающими от ИГ, брать отсчеты мгновенных значений функции ƒ(t), т.е. определять величины ƒ_k и выдавать короткие импульсы с площадью, пропорциональной ƒ_k. Кроме того, требуется, чтобы эти импульсы, во-первых, получали требуемый знак, а во-вторых, чтобы они поочередно поступали на два выхода устройства, т.е. чтобы, например, импульсы четных номеров поступали на верхний выход, а нечетных номеров — на нижний. Далее следуют фильтры нижних частот ФНЧ с верхней граничной частотой . Затем идут два перемножителя П, на вторые входы которых поступают сдвинутые по фазе на π/2 напряжения частоты ω₁ = ω₀ + ω_с от двухфазного генератора Г. Напряжения, снимаемые с обоих перемножителей, складываются.

Описанная схема интересна тем, что в ней отсутствует широкополосный фазовращатель. Однако для получения хороших результатов нужно, по-видимому, предъявить строгие требования к фильтрам нижних частот.

 

предыдущая                           оглавление                      следующая