§ 3. Спектры; определения и классификация

 

Вернемся к формуле (2.2) ряда Фурье и перепишем ее в виде

 

 

 

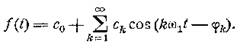
Здесь ω₁ = 2π/T — основная частота. Как мы видим, сложная периодическая функция f(t) вполне определяется совокупностью величин c_k и φ_k. Совокупность величин c_k носит название спектра амплитуд. Совокупность величин φ_k называется соответственно спектром фаз. Для многих применений достаточно знать спектр амплитуд; он применяется настолько часто, что когда говорят просто спектр, то подразумевают обычно именно амплитудный спектр. В остальных случаях делают соответственные оговорки. Мы будем поступать так же.

Спектр периодической функции можно изобразить графически. Выберем для этого координаты c_k и ω = kω₁. Спектр будет изображен в этой системе координат совокупностью дискретных точек, так как каждому значению kω₁ соответствует одно определенное c_k. График, состоящий из отдельных точек, неудобен.

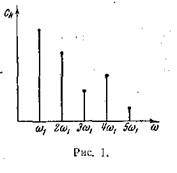
Поэтому принято изображать амплитуды отдельных гармоник вертикальными отрезками соответствующей длины. В результате спектр периодической функции принимает вид, показанный на рис. 1. Это — дискретный спектр; его называют также линейчатым, заимствуя этот термин из оптики. Второе свойство спектра, изображенного на рис. 1, состоит в том, что этот спектр — гармонический. Это значит, что он состоит из равноотстоящих спектральных линий; частоты гармоник находятся в простых кратных соотношениях. Конечно, отдельные гармоники, иногда даже первая, могут отсутствовать, т.е. амплитуды их могут равняться нулю; это, однако, не нарушает гармоничности спектра.

Не следует думать, что только периодическая функция обладает дискретным спектром. Предположим, например, что сложное колебание есть результат сложения двух синусоидальных колебаний с несоизмеримыми частотами, скажем ω₁ и ω₁. Это колебание заведомо непериодическое, однако спектр его дискретен и состоит из двух спектральных линий.

Функция, обладающая дискретным спектром из произвольно расположенных на шкале частот спектральных линий, называется почти-периодической и обладает многими интересными свойствами[1].

Итак, дискретные, или линейчатые спектры могут принадлежать как периодическим, так и непериодическим функциям. В первом случае линейчатый спектр обязательно гармонический.

Большое практическое значение имеет частный случай почти-периодической функции, представляемой разложением вида

,

где k принимает как положительные, так и отрицательные значения. Спектр, отвечающий этому разложению, характеризуется тем, что линии его эквидистантны; поэтому мы будем называть такого рода линейчатый спектр квазигармоническим. Таковы, например, спектры периодически модулированных колебаний; ω₀ в этом случае есть не что иное, как несущая частота.

Обратимся теперь к спектрам непериодических функций. Мы уже знаем, что в результате предельного перехода от ряда к интегралу Фурье интервалы между отдельными спектральными линиями неограниченно сокращаются, линии сливаются, и вместо дискретных точек спектр должен изображаться непрерывной последовательностью точек, т.е. непрерывной кривой. Такого рода спектр называется сплошным.

Здесь нужно однако внести одно уточнение. Мы писали формулу интеграла Фурье в виде (2.10):

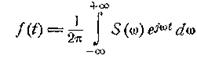
Подынтегральная функция выражает отдельное, бесконечно малое слагаемое, т.е. колебание с бесконечно малой амплитудой dC:

Отсюда находим

 

Таким образом, величина S(ω) выражает не непосредственно амплитуду, а так называемую спектральную плотность. Однако обычно эту деталь опускают и называют S(ω) комплексным спектром непериодической функции, а абсолютное значение (модуль) этой величины

Φ(ω) =│S(ω)│

просто спектром. Это может повести к недоразумениям лишь в том случае, когда мы будем непосредственно сравнивать соотношения для периодических и непериодических функций.

Итак, мы имеем две основные разновидности спектров: линейчатые и сплошные. Гармонические линейчатые спектры принадлежат периодическим функциям, сплошные — непериодическим.

В заключение настоящего параграфа заметим, что теми или иными функциями времени могут выражаться изменения самых различных физических величин. Соответствующий смысл получают и спектры этих функций. В практике приходится, например, иметь дело со спектрами механических величин: смещения, скорости, ускорения, силы, давления и т. п.; электрических величин: тока, напряжения и т. п. Кроме того, нас часто интересуют спектры квадратичных величин: мощности или энергии. Например, в оптике чаще всего имеют дело со спектрами этих величин.

 

 

предыдущая                           оглавление                      следующая