§ 12. Связь
между длительностью импульса и шириной его спектра
Мы уже установили, что чем
короче импульс, тем шире его спектр, в частности, бесконечно короткий импульс
имеет бесконечно протяженный спектр с равномерной плотностью. В этом
проявляется одно весьма общее и имеющее очень большое значение соотношение, к
установлению которого мы подойдем постепенно.
Прежде всего
заметим, что общее представление о связи между протяженностями во времени и по
частоте вытекает непосредственно из общего свойства преобразования Фурье.
Положим, что функция ƒ(t)
имеет спектр S(ω). Изменим
масштаб времени в a раз,
и найдем спектр функции aƒ(at) (множитель a перед
функцией добавлен для сохранения площади, т.е. размеры графика функции
увеличены по оси ординат во столько же раз, во сколько уменьшены в связи с
изменением масштаба размеры по оси абсцисс)
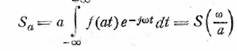
Таким образом, если длительность функции ƒ(t) уменьшена в a раз, то ровно во столько же раз возрастает ширина
спектра функции. При этом предполагается, что определения длительности функции
и ширины её спектра остаются неизменными.
Теперь рассмотрим несколько примеров.
Возьмем снова
прямоугольный импульс [см. § 11, формулу (11.4) и рис. 18]. Для спектра такого
импульса мы получили
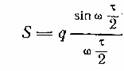(12.1)
Сопоставим теперь длительность импульса и ширину его
спектра. Под длительностью импульса ∆t естественно
в данном случае понимать величину τ. Что касается ширины спектра, то здесь нужно выбрать
какое-либо определение, так как спектр импульса безграничен. Но так как спектр
убывает с частотой, то можно, например, условиться считать за ширину спектра
полосу частот ∆ƒ между нулем и тем
значением частоты, когда спектр первый раз обращается в нуль. Из формулы (12.1)
видно, что это случится, когда аргумент синуса будет равен π..
Отсюда следует равенство
или
∆ƒ∆t =
1,
т.е. произведение длительности данного импульса
∆t на ширину его спектра
∆ƒ (в выбранном нами произвольном
определении) равно единице.
Для треугольного импульса мы получили
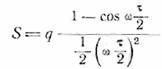(12.2)
Первый нуль спектра будет при
откуда
∆ƒ∆t=2
Мы сохраняем определения для
∆ƒ и ∆t;
∆ƒ — полоса
частот до первого перехода спектра через нуль, ∆t
— интервал, вне которого функция, представляющая импульс, равна нулю.
Для косинусоидального
импульса
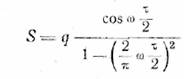(12.3)
и искомое соотношение принимает вид
∆ƒ∆t =
1,5
Для всех рассмотренных примеров
получается, что
∆ƒ∆t ≈ 1 (12.4)
Однако, если бы мы захотели увеличить число примеров, то скоро
натолкнулись бы на затруднение при выборе определений ∆ƒ и ∆t для
данного конкретного случая. Положим, например, что мы желаем установить
соотношение типа (12.4) для экспоненциального импульса
ƒ(t)= 
Предыдущее определение∆t непригодно, так как очевидно, что эта функция не
равна нулю в интервале от 0 до ∞. Спрашивается, как же определить длительность
некоторым универсальным образом?
Прежде всего заметим, что вопрос о соотношении между ∆ƒ и ∆t имеет не только теоретическое, но и очень большое
практическое значение. В современной импульсной технике необходимо создавать
очень короткие, но в то же время очень мощные импульсы. Иначе говоря, в
импульсе большая энергия должна быть сосредоточена в малом интервале времени.
С другой стороны,
требуется, чтобы спектр импульса был как можно менее
размыт, поскольку широкий спектр вызывает целый ряд серьезных трудностей в
устройстве импульсной аппаратуры.
Таким образом, с одной стороны, мы
требуем малого ∆t, а с
другой — малого ∆ƒ. Эти требования, как мы
видели, вообще говоря, противоречивы. Однако можно искать вид импульса, для
которого произведение ∆ƒ∆t имеет наименьшее значение.
Если подходить к
вопросу об определении величин ∆ƒ и
∆t с практической точки зрения, то
можно предложить следующее определение длительности: под длительностью импульса
понимается промежуток времени, в котором сосредоточена подавляющая часть
энергии импульса. Аналитически это определение можно сформулировать так:
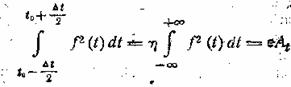(12.5)
Здесь
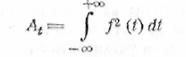
— величина,
пропорциональная полной энергии импульса; η — выражаемая
правильной дробью относительная доля полной энергии импульса, приходящаяся на
промежуток времени ∆t. Уравнение (12.5) может с
удобством решаться при помощи планиметрирования.
Аналогичным образом
можно определить и ширину спектра
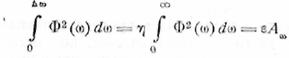(12.6)
Заметим, что по теореме Рэйли
Aω = πAt. (12.7)
Что касается величины t0, входящей в пределы интеграла в левой части (12.5),
то в ряде случаев выбор этой величины не оставляет сомнений. Для симметричных
импульсов, выражаемых четными функциями, t0 = 0. Для импульсов, начинающихся при t = 0, формулу (12.5) следует переписать в виде
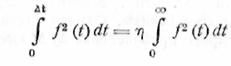
Вернемся к ранее
рассмотренным импульсам и вычислим их длительности и ширины их спектров,
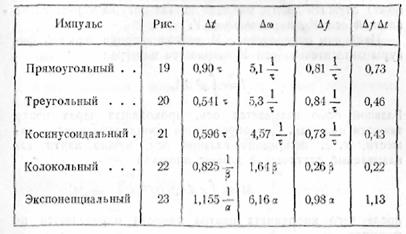
основываясь на предложенном определении. Выбирая для η значение 0,9 получим следующую сводную таблицу интересующих
нас величин (детали вычислений вынесены в добавление VI в конце книги).
Мы ограничимся лишь одним замечанием по поводу этой таблицы: как видим, ∆ƒ∆t оказывается наибольшим для импульсов,
характеризующихся разрывом функции ƒ(t) (прямоугольный
и экспоненциальный); меньшее значение ∆ƒ∆t получается для импульсов с разрывом в первой
производной (треугольный и косинусоидальный) и,
наконец, наименьшее ∆ƒ∆t оказывается
у колокольного импульса, отличающегося тем, что выражающая его функция
непрерывна со всеми своими производными.
Из всего изложенного можно
заключить, что связь между ∆ƒ
и ∆t удовлетворяет в общем случае
неравенству
∆ƒ∆t ≥ µ, (12.8)
где µ — некоторая постоянная, зависящая, конечно, от выбора
определений ∆ƒ и ∆t.
Определения, которыми мы
только что воспользовались, при всей их простоте и практическом удобстве не
позволяют, к сожалению, поставить и разрешить вопрос в общем виде. Мы введем
новые определения для ∆ƒ
и ∆t, основанные
на применении понятия о моментах функции.
Для большей наглядности
поясним эти определения ссылкой на общеизвестные понятия и определения
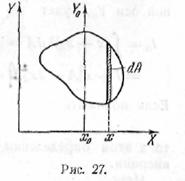
технической механики. Предположим, что нам
дана произвольная плоская фигура в плоскости XY, и требуется некоторым универсальным образом
определить размер этой фигуры в направлении оси X (рис.
27). Таким универсальным измерителем может служить радиус инерции данной
фигуры относительно главной оси Y0,
параллельной Y.
Напомним определения.
Моментом инерции плоской фигуры относительно оси Y называется
интеграл
Главной осью называется ось,
проходящая через центр тяжести площади. Для определения координаты центра
тяжести, т.е. положения главной оси, нужно найти так называемый статический
момент площади
после чего координата центра тяжести определяется по
формуле
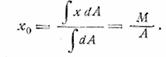
Главный момент инерции, т.е. момент относительно главной
оси Y0 будет
Если положить
I0 = r2 A,
то в этом определении величина r и называется радиусом инерции.
Итак,
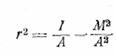( 12.9)
и определенная таким образом величина может служить
универсальной мерой ширины данной фигуры в направлении оси X..
Обратимся теперь к
импульсам и их спектрам. Графики как тех, так и других являются плоскими
фигурами, к которым в полной мере применимо все сказанное выше. Для импульсов
роль оси X выполняет ось времен, для спектров — ось частот.
Элемент площади фигуры выразится произведением
значения функции на дифференциал независимой переменной. Однако, ввиду того что нам встречаются и знакопеременные функции,
удобнее оперировать не самой функцией, а ее квадратом.
Таким образом, можно ввести следующие
обозначения и определения:
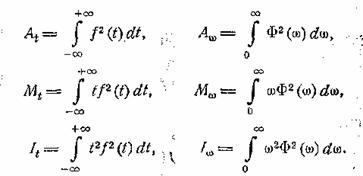
Далее, согласно (12.9)
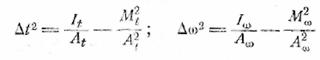
Отсюда
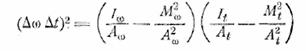
или, используя (12.7) и вводя 
,
(12.10)
Теперь ограничим и упростим задачу, предположив, что
речь идет о четных функциях времени. Тогда
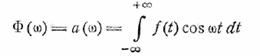
и, кроме того,
t0 = 0; Mt = 0.
Условимся, далее, что функция ƒ(t) нормирована, т.е. что
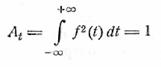
и соответственно
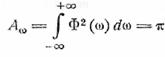
Займемся теперь
интегралом
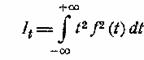
Мы имеем
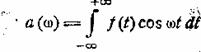
Продифференцируем обе части по ω
,
где b1(ω) —
спектр нечетной функции
ƒ1(t) = tƒ(t).
Воспользовавшись теоремой Рэйли, получим
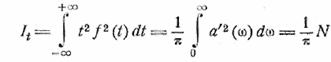
Введя все эти соотношения в
(12.10), находим (индекс ω
здесь и далее опущен)
. (12.11)
Поставим
себе теперь задачу найти наименьшее значение ∆ƒ∆t, т.е. подобрать такую функцию, которая дает минимальное значение интегральному выражению
К = N(πI ─
M2) (12.12)
Воспользуемся для этой цели, следуя Майеру и Леонтович
[11], вариационными методами.
Составим первую вариацию величины
(12.12):
.
Для нахождения минимума мы должны приравнять эту
вариацию нулю. Но при этом интегралы I, M и N примут вполне
определенные постоянные значения, которые мы обозначим соответственно через i, m и n. После
этого мы можем объединить варьируемые интегралы и записать
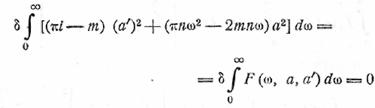
Теперь мы можем записать уравнение Эйлера
в следующем виде:
(12.13)
Умножим это уравнение на a и проинтегрируем от нуля до бесконечности. Интеграл в
первом члене возьмем по частям
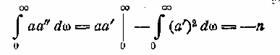
[так как a(∞) = a´(0) = 0].
Интегрируя второй член, заметим, что
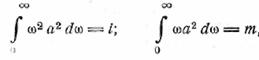
и таким образом мы получим соотношение
2πi = 3m2.
Замечая, что согласно (12.12)
мы можем теперь записать
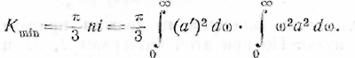
Для оценки этого выражения обратимся к неравенству Буняковского
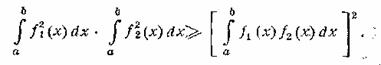
В нашем случае
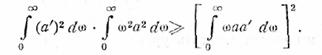
Вычисляя интеграл в правой части
неравенства по частям, найдем, что он равен – π/2.
Таким образом,
и
,
откуда, наконец,
0,046.
Мы получили, таким образом, оценку ∆ƒ∆t для
наивыгоднейшего случая. Интересно сопоставить
полученную величину со значением ∆ƒ∆t для колокольного импульса, для которого, как мы
видели, из всех рассмотренных нами импульсов произведение ∆ƒ∆t получается
наименьшим. Нельзя, понятно,
воспользоваться ранее вычисленными данными, так как сейчас мы пользуемся
совершенно другими критериями. Мы должны вычислить интегралы, входящие в
формулу (12.11).
Колокольный импульс и
его спектр были определены выше (§ 11):
Из условия нормировки
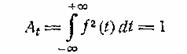
определяем β = 
. После этого находим:
Подставляя эти значения в
формулу (12.12), получим
= 0,048.
Эта величина, как видим, очень близка к теоретическому
минимуму.
предыдущая оглавление следующая
